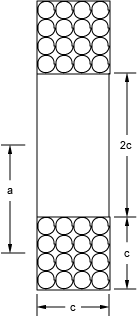
A Brooks Coil is generally known as a special case of the circular coil inductor of rectangular cross section that is implemented to achieve the maximum inductance with a given length of wire. As can be seen from the picture below, the coil has a square cross section and the inner diameter is equal to twice the height (or width) of the coil winding.

The inductance for a Brooks coil can be found from the following equation:

where c is the height and width of the coil winding (in cm) and N is the number of turns. A second formula is shown below (Grover, Frederick W., Inductance Calculations Working Formulas and Tables, D. Van Nostrand Company, 1946, p98. ISBN:0486495779):

where a is the mean radius of the inductor (in cm) and N is the number of turns.

The calculator below can be used to determine the inductance values for a specific Brooks coil configuration (Coil height/width and number of turns) using the first formula above. It will also determine the inner, outer, and mean radii based on that geometry. Credit for the initial Javascript code used in the calculator is given to Ray Allen who has a number of similar useful calculators on his website, Pulsed Power Portal.