The equations, diagrams, and waveforms on this page describe resonant charging of one capacitor from another capacitor through a charging inductor. This form of charging is frequently used in pulsed power and power conditioning circuits in order to efficiently transfer energy from one stage to another. The following equations are used to describe the critical parameters of resonant charging, including the resonant frequency (omega), the charging current, the voltage on the load capacitor, the maximum possible load capacitor voltage, and the efficiency of the energy transfer.
Each of the waveform plots shown below can be clicked
on to open up the full size version of the graph in a separate window.
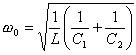 |
|
L is the circuit inductance
(H)
C1 is the source capacitance (F) C2 is the load capacitance (F) |
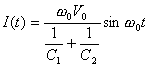 |
|
V0 is the initial voltage on the C1 capacitor (V) |
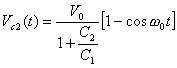 |
|
Same as above |
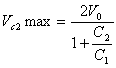 |
|
Same as above |
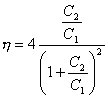 |
|
Same as above |
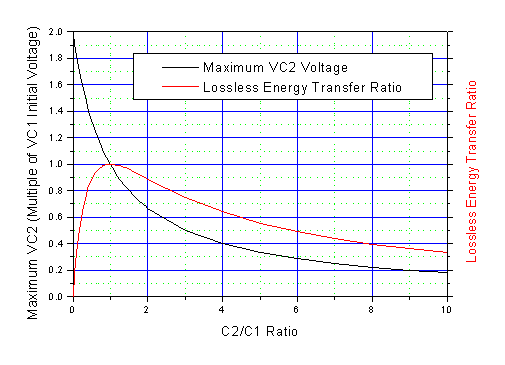
The following graph illustrates the relationship
between these last two parameters (Maximum C2 Voltage and Energy
Transfer Efficiency) and the ratio of capacitances (C2 / C1).One
can see from the graph that maximum energy transfer is obtained when the
two capacitances are equal. A second condition of interest is that where
the load capacitance is much smaller than the source capacitance. In this
case, the maximum load capacitor voltage approaches 2 times the initial
voltage on the source capacitor. A voltage gain of ~2X is therefore
possible during the resonant charging. This can be used in many cases to
reduce the operating voltage of the front end power system.
Matched Capacitance Resonant Charging (C2=C1)
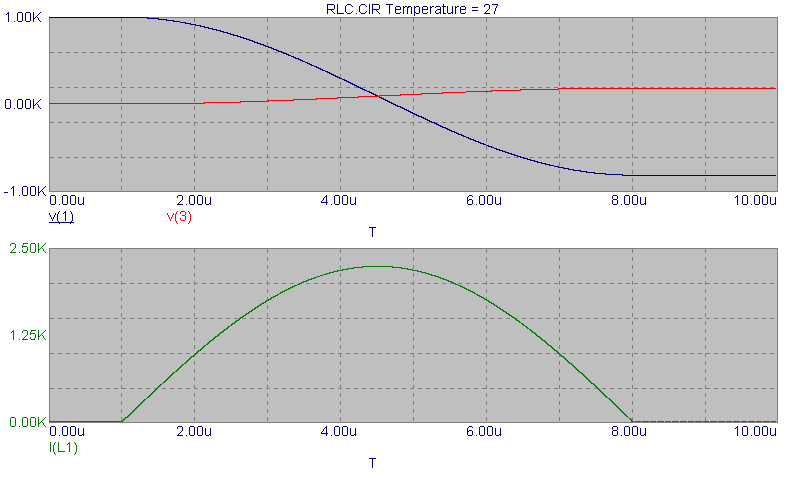
As noted above, this case allows maximum energy transfer from the source capacitor to the load capacitor. All of the energy from C1 can be transferred to C2. Since the capacitors are equal, this implies that the voltage on C2 will equal the initial voltage on C1 (as shown in the waveforms). The voltage on the source capacitor also reaches zero volts at the same time that the load capacitor reaches its maximum voltage. In real life, resistive losses in the circuit will reduce the maximum possible voltage on C2 somewhat. One can also see that the charging current in this case is a simple half-sinusoid shape.
The viewer should also note that the simulation has
assumed that the switch has opened at the end of the half-period (this
has been done in all three cases). If this were not done, the energy would
merely resonantly transfer back to the source capacitor. In real life,
this can be done by several techniques including the addition of a diode
to the circuit to only allow energy transfer in the forward direction.
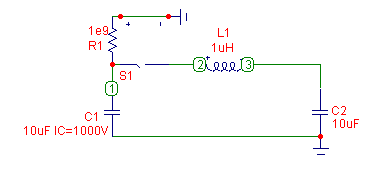
Ring-Up Resonant Charging (C2<<C1)
This is the second case of interest since as noted above, the voltage on the load capacitor can be doubled providing a voltage gain in the system of 2X. In this case, the load capacitor voltage is approximately doubled (~1.8X) as the source capacitor voltage only drops by ~10%.
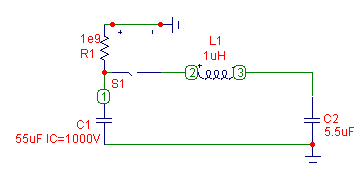
Ring-Down Resonant
Charging (C2>>C1)
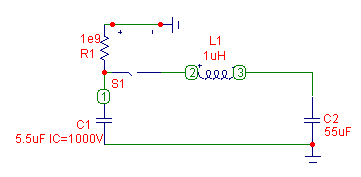
Send consulting inquiries, comments, and suggestions to
nessengr@san.rr.com
[BACK] [HOME] [RESUME] [PUBLICATIONS] [NEWS] [LINKS] [CAPABILITIES] [TECHDATA]
Ness Engineering, Inc.
P.O. Box 261501
San Diego, CA 92196
(858) 566-2372
(858) 240-2299 FAX
© Richard M. Ness and Ness Engineering, Inc. |
Website File Auto-Update Javascript courtesy of www.javafile.com Download the Script